STRUKTUR DATA - B Tree and Heap & Deap

B-Tree

Pada B-Tree dikenal istilah order. Order menentukan jumlah maksimum/minimum anak yang dimiliki oleh setiap node, sehingga order merupakan hal yang cukup penting dalam B-Tree. 2-3 Tree pada postingan sebelumnya yaitu Balanced Binary Search Tree (AVL and RBT) and 2-3 Tree merupakan salah satu B-Tree berorder 3. Itu sebabnya setiap nodenya memiliki batasan anak, dengan minimal 2 anak dan maksimal 3 anak.

Aturan pada B-Tree : m = order

• Setiap node (kecuali leaf) memiliki anak paling banyak sejumlah m anak
• Setiap node (kecuali root) memiliki anak paling sedikit m/2 anak
• Root memiliki anak minimal 2, selama root bukan leaf
• Jika node non leaf memiliki k anak, maka jumlah data yang tersimpan dalam node k-1
• Data yang tersimpan pada node harus terurut secara inorder
• Semua leaf berada pada level yang sama, level terbawah

Berikut contoh B-Tree :

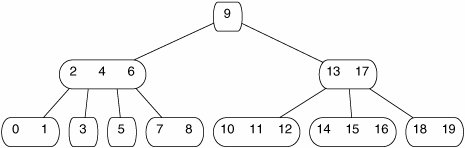B-Tree order 4

B-Tree order 6

Operasi : Searching

Searching pada B-Tree mirip seperti 2-3 Tree. Pertama-tama kita bandingkan dengan rootnya terlebih dahulu kemudian cek apakah sama dengan rootnya atau lebih kecil atau lebih besar atau bahkan diantara rootnya (jika root memiliki lebih dari 1 data).

berikut ini adalah codingannya dalam C :

Operasi : Insertion

Aturan Insertion :

• Anggap data yang mau di insert adalah key
• Posisikan key pada node yang sesuai, seperti pada BST dan 2-3 Tree, anggap node tersebut A
• Jika A adalah node dengan jumlah data kurang dari m-1, maka langsung masukan saja
• Jika A adalah node dengan jumlah data m-1, maka masukan nilai tengah kemudian masukan ke parentnya. Kemudian anggaplah parent tersebut A. Kemudian periksa kembali sesuai aturan point ke 3 dan 4.

contoh :

gambar dibawah ini adalah operasi insertion pada b-tree berorder 5

Operasi : Deletion 

Aturan Deletion :

• Anggap node yang mau di delete adalah key
• Delete dilakukan pada leaf. Meskipun pada saat menghapus node parent, kita tetap menganggapnya menghapus leaf, karena ketika parent dihapus lalu digantikan oleh anak terbesar subtree kiri atau anak terkecil subtree kanan sama saja kita seolah-olah menghapus anak yang menggantikannya. dimana anak tersebut selalu berada pada posisi leaf. maka leaf tersebut dianggap P.
• Jika ukuran P > m/2 maka langsung delete saja data yang ingin dihapus
• Jika ukuran P = m/2 maka : perhatikan siblingnya (anggap sibling adalah Q)
• Q > m/2, maka rotasi pada P
• Q = m/2, satukan P dan Q

contoh :

delete pada b-tree order 5

Heap and Deap

heap 

Heap adalah complete binary tree yang berbasis struktur data dan memenuhi aturan heap. Tree pada heap and deap tidak memenuhi aturan BST yang harus terurut secara inorder, yang penting tree tersebut mengikuti aturan heap.

Ada 2 jenis heap :

1. Min Heap : node paling kecil adalah root dan semakin kebawah levelnya semakin besar
2. Max Heap : node paling besar adalah root dan semakin kebawah levelnya semakin kecil
3. Min-Max Heap : min-heap dan max-heap levelnya saling bergantian pada tree

contoh :

kiri : min heap   -------   kanan : max heap

Heap biasanya diimplementasi kan pada array dan indexnya dimulai dari 1, bukan 0.

cara mengetahui lokasi index parent dan child :

• Parent(x)  = x / 2      dengan x = index anak
• Left-child(x)  = 2 * x      dengan x =  index parent
• Right-child(x)  = 2 * x + 1      dengan x = index parent

Min Heap

Operasi : Find Min

Pada min-heap, untuk menemukan node terkecil sangatlah mudah, karena root dari min heap adalah node dengan nilai terkecil.

Operasi : Insertion

• Insert node baru (key) pada index selanjutnya (setelah index terakhir)

• lakukan upheap, yaitu compare key dengan parentya, jika node parent > key, maka swap. Jika tidak maka biarkan saja

• lakukan point ke-2 berulang kali jika setelah diswap masih parent > key. namun stop jika key sudah berada pada posisi root.

contoh :

insert 5

insert 20

Operasi : Deletion

aturan delete :

• operasi delete hanya terjadi pada rootnya saja. 

• gantikan elemen yang didelete dengan node yang berada pada index terakhir

• lakukan downheap, yaitu compare dengan salah satu childnya yang terkecil. jika node tersebut > child terkecil, maka swap

• lakukan point ke-3 jika setelah diswap node tersebut masih memiliki anak. Namun stop jika node sudah dalam posisi leaf atau node tersebut < child terkecilnya

contoh :

delete node 7

node 7 dihapus kemudian diganti oleh node index terakhir, yaitu 28
kemudian 28 di compare dengan anak terkecilnya 10

28>10, maka swap
kemudian 28 dicompare lagi dengan anak terkecilnya, 12.
28>12, swap kembali. karena 28 sekarang pada posisi leaf. maka updown dihentikan

Max Heap

Max heap adalah kebalikan dari min heap.

Operasi : Find Max

Pada max-heap, untuk menemukan node terbesar sangatlah mudah, karena root dari max heap adalah node dengan nilai terbesar.

Operasi : Insertion

• Insert node baru (key) pada index selanjutnya (setelah index terakhir)
• lakukan uphead, yaitu compare key dengan parentnya, jika node parent < key maka swap. Jika tidak maka biarkan saja
• lakukan point ke-2 berulang kali jika setelah diswap masih parent < key. namun stop jika key sudah berada pada posisi root.

contoh :

insert 15

pada saat di insert 15, kemudian dicompare dengan parentnya ternyata 15>7, maka swap
kemudian setelah diswap dicompare lagi dengan parentnya ternyata 15>14, maka diswap lagi

Operasi : Deletion

aturan delete :

• operasi delete hanya terjadi pada rootnya saja. 
• gantikan elemen yang didelete dengan node yang berada pada index terakhir
• lakukan downheap, yaitu compare dengan salah satu childnya yang terbesar. jika node tersebut < child terbesar, maka swap
• lakukan point ke-3 jika setelah diswap node tersebut masih memiliki anak. Namun stop jika node sudah dalam posisi leaf atau node tersebut > child terbesarnya

contoh :

delete 20

20 akan digantikan oleh 15, karena 15 berada pada index terakhir

15 dibandingkan dengan parentnya. ternyata 15<34, maka tidak diswap dan operasi insertion selesai

Min-Max Heap

Min-Max Heap adalah penggabungan dari min-heap dan max-heap. dimana pada tree ini kita dapat mendapatkan 1 angka terkecil dan 2 angka terbesar. Namun sayangnya, angka terbesar tersebut salah satunya memang terbesar tetapi satunya lagi belum pasti nilai terbesar keduanya.

berikut contohnya :

level pertama pada min-max heap adalah min level dan bawahnya max level.

nilai terkecil pada tree terletak pada rootnya sedangkan 2 nilai terbesarnya adalah anak dari rootnya.

Operasi : Insertion

• Insert node baru (key) pada index selanjutnya (setelah index terakhir)

• jika key terletak pada level min : bandingkan dengan parentnya

• Jika parent < key maka swap dan upheapmax dari parentnya (dibandingkan dengan grandparentnya dari posisi key setelah swap)

• Jika parent > key, upheapmin dari posisi key (dibandingkan dengan grandparentnya dari posisi key).

• jika key terletak pada level max :

• Jika parent > key maka swap dan upheapmin dari parentnya (dibandingkan dengan grandparentnya dari posisi keysetelah swap)

• jika parent < key, upheapmax dari posisi key(dibandingkan dengan grandparentnya dari posisi key).

Operasi : Deletion
ada 2 jenis delete, yaitu delete min, dan delete max

• Delete Min, menghapus node terkecil, yaitu root

• Delete Max, menghapus node terbesar, yaitu salah satu dari anak root

konsep deletenya sama :

• node yang dihapus digantikan oleh node index terakhir

• lakukan downheapmin jika delete min, atau downheapmax jika delete max

Deap

Deap adalah gabungan dari min heap dan max heap, namun berbeda dengan min-max heap, karena pada deap, rootnya tidak ada, atau kosong/NULL dan subtree kirinya adalah min heap dan subtree kanannya adalah max heap.

contoh :

pada deap, dikenal istilah partner, yaitu pasangan node

pada gambar diatas, pasangannya dapat dilihat dari warnanya

5  -->45

10-->25

8  -->40

15-->20

19-->22

9  -->40

30-->40

mengapa partner 9 dan 30 adalah 40?? karena jika suatu node tidak memiliki pasangan pada subtree kanan atau sebaliknya, maka node tersebut dipasangkan dengan parent dari node yang seharusnya. pada node 9 seharusnya dipasangkan dengan node dengan imdex 14, tapi karena node index 14 tidak ada/NULL maka dipasangkan dengan 40 yang merupakan induk dari node index 14.

Operasi : Insertion

• masukkan node baru pada index selanjutnya (setelah index terakhir)
• jika key terletak pada min heap 
• bandingkan dengan max partner
• jika max partnernya < key, swap
• lakukan min upheap, yaitu up heap di min subtree
• jika key terletak pada max heap 
• bandingkan dengan min partner
• jika min partnernya > key, swap
• lakukan max upheap, yaitu up heap di max subtree

contoh :

insert 50

Operasi : Deletion

• ada 2 jenis delete, delete min dan delete max
• jika delete min
• gantikan node yang dihapus dengan node index terakhir
• lakukan downheap min
• compare dengan partnernya, jika partner < node tersebut, swap
• jika delete max
• gantikan node yang dihapus dengan node index terakhir
• lakukan downheap max
• compare dengan partnernya, jika partner > node tersebut, swap

contoh :

delete 5