STRUKTUR DATA - Balanced Binary Search Tree (AVL and RBT) and 2-3 Tree

Balanced Binary Search Tree

Dalam Binary Search Tree, tinggi maksimal suatu tree adalah N-1, dimana N  adalah jumlah node. Dalam melakukan suatu operasi, misalnya insertion, deletion, dan seaching, kecepatan waktu merupakan hal yang cukup penting untuk diperhatikan. Setiap operasi pasti di harapkan dapat berjalan dengan cepat, sehingga semakin cepat suatu operasi maka semakin baik. Cepat atau tidaknya suatu operasi, bergantung pada ketinggian tree tersebut, semakin rendah tingginya, maka semakin cepat.

Dengan Balanced Binary Search Tree, kita dapat membuat suatu tree dengan tinggi minimum.
untuk menetapkan tingginya, kita dapat menggunakan rumus berikut:

O(log n)

2 contoh tree yang termasuk ke dalam balanced binary search tree, yaitu :

- AVL Tree

- Red Black Tree (RBT)

AVL Tree

AVL adalah balanced binary search tree dimana ia memiliki perbedaan jumlah node pada subtree kiri dan subtree kanannya maksimal 1 (atau dapat dikatakan antara tingginya sama atau selisih satu).

Berikut gambarannya :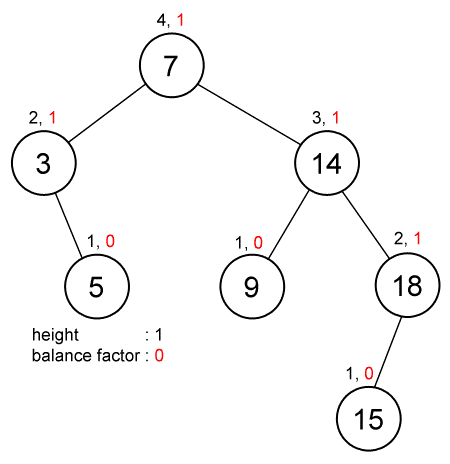

AVL Tree, karena factor tertingginya 1

Not AVL Tree, karena  balance factor tertingginya 2, sedangkan syarat AVL adalah selisihnya maksimal 1

Note :

Cara menentukan Height dan Balance Factor :

Height :
- Jika node (root) tidak memiliki subtree heightnya = 0
- Jika node adalah leaf, height =  1
- Jika internal node, maka height =  height tertinggi dari anak + 1

Balance Factor :
-selisih height antara anak kiri dan kanan, jika tidak memiliki anak, dianggap 0.

AVL Tree Operations : Insertion

Insert suatu node pada AVL sama halnya pada insert node pada binary search tree, dimana node baru diposisikan sebagai leaf. Setelah memasukkan node baru, maka harus dilakukan penyeimbangan kembali pada path dari node yang baru di insert atau path terdalam. Namun biasanya, path terdalam adalah path dari node yang baru saja di insert.

Ada 4 kasus yang biasanya terjadi saat operasi insert dilakukan, yaitu :

anggap T adalah node yang harus diseimbangkan kembali

- Kasus 1 : node terdalam terletak pada subtree kiri dari anak kiri T (left-left)
- Kasus 2 : node terdalam terletak pada subtree kanan dari anak kanan T (right-right)
- Kasus 3 : node terdalam terletak pada subtree kanan dari anak kiri T (right-left)
- Kasus 4 : node terdalam terletak pada subtree kiri dari anak kanan T (left-right)

Ke-4 kasus tersebut dapat diselesaikan dengan melakukan rotasi
- Kasus 1 dan 2 dengan single rotation
- Kasus 3 dan 4 dengan double rotation

Single Rotation

Single rotasi (rotasi 1x) dilakukan apabila searah, left-left atau right-right

Gambaran Single Rotation :

Single Rotation
pada contoh diatas, left-left karena dari 30 ke 22 ke kiri, dan dari 22 ke 15 ke kiri juga

Double Rotation

Double rotasi (rotasi 2x) dilakukan apabila searah, left-right atau right-left.

Gambaran Double Rotation :

Step 1 (Rotasi pertama)
kasus diatas adalah left-right

Step 2 (Rotasi kedua)

kasus diatas, left-left

AVL Tree Operations : Deletion

Operasi penghapusan node sama seperti pada Binary Search Tree, yaitu node yang dihapus digantikan oleh node terbesar pada subtree kiri atau node terkecil pada subtree kanan. Jika yang dihapus adalah leaf, maka langsung hapus saja. Namun jika node yang dihapus memiliki child maka childnya yang menggantikannya. Namun setelah operasi penghapusan dilakukan, cek kembali apakah tree sudah seimbang atau belum, jika belum maka harus diseimbangkan kembali. Cara menyeimbangkannya pun sama seperti insertion.

delete node 60

node 55 tidak seimbang, karena anak kiri 0 dan anak kanan 2, selisih 2.
diseimbangkan dengan single rotation (left-left) karena 55 ke 65 kiri dan 65 ke 70 kiri
akan tetapi, node 50 menjadi tidak seimbang, di subtree kiri 4 dan subtree  kanan 2

diseimbangkan dengan double rotation (left-right) karena dari 50 ke 25 kiri dan 25 ke 40 kanan

AVL yang sudah balance

Red Black Tree (RBT)

Suatu tree dikatakan RBT apabila :
- setiap node memiliki warna (hitam atau merah)
- root berwarna hitam
- eksternal node berwarna hitam
- node merah tidak memiliki anak merah
- setiap path memiliki jumlah node hitam yang sama dengan path lainnya

berikut contoh RBT :

RBT operations : Insertion

aturan  insertion :

- node baru berwarna merah

- node merah tidak boleh memiliki anak merah

apa yang dilakukan jika node merah memiliki node child merah?

cek uncle/paman dari node merah (anak)

1. jika uncle berwarna merah, maka ubah warna parent dan uncle menjadi hitam, dan grand parent menjadi merah.
2. jika uncle berwarna hitam, lakukan rotasi single/double, kemudian setelah rotasi, parent berwarna hitam, anak berwarna merah
3. jika tidak memiliki paman, maka defaulnya adalah hitam (dilihat dari external nodenya). sehingga mengikuti aturan kedua (uncle hitam)

contoh 1 :

insert node x, parent-y- merah memiliki child -x- merah, maka melanggar aturan.
lihat unclenya, -d- berwarna merah, maka mengikuti aturan pertama
y dan d menjadi hitam, kemudian z sbg grand parent berwarna merah

contoh 2 :

insert node x, parent-y- merah memiliki child -x- merah, maka melanggar aturan.
lihat unclenya, karena tidak memiliki uncle maka ikuti aturan ketiga
rotasi yang dilakukan pun sama seperti AVL. pada kasus diatas dilakukan single rotation 

contoh 3 :

insert node y, parent-x- merah memiliki child -y- merah, maka melanggar aturan.
lihat unclenya, karena tidak memiliki uncle maka ikuti aturan ketiga
rotasi yang dilakukan pun sama seperti AVL. pada kasus diatas dilakukan double rotation 

RBT operations : Deletion

Deletion RBT sama seperti deletion pada AVL
aturannya :

anggap M =  node yang di delete dan C = node yang menggantikan

1. jika M merah, diganti dengan C yang berwarna hitam
2. jika M hitam dan C merah, maka M diganti C dan C berubah warna menjadi hitam
3. jika M hitam dan C hitam, kita lakukan pemisalan kembali :

  C = N,
  P = parent N,
  S = sibling N,
  Sl = anak kiri S,
  Sr = anak kanan S

  kita perhatikan siblingnya :
  a.  jika S merah, ubah warna N dan P (tukar warna), kemudian rotate di P
  b.  jika S hitam dan Sl, Sr hitam, maka ubah S menjadi merah
  c.  jika S hitam dan Sl atau Sr ada yang merah maka lakukan rotasi single/double

contoh 1 :

kita akan menghapus node 3

karena node 3 adalah leaf dan berwarna merah, maka langsung hapus saja. tapi jika 5 merah dan kedua anaknnya 3 dan 6 hitam, maka ketika node 3 dihapus, 5 dan 6 bertukar warna menjadi 5 merah dan 6 hitam

contoh 2 :

pada kali ini kita akan menghapus node 8, karena node 8 memiliki anak, maka yang menggantikannya adalah anaknya, pada kali ini kita mengambil anak kanan terkecil, yaitu 9. pada penghapusan node ini mengikuti aturan pertama

node 9 menggantikan posisi 8, dan node 9 berubah jadi merah. setelah dihapus node 8, terjadi ketidakseimbangan di node 9, pada subtree kiri 9, ada 2 anak, sedangkan subtree kanannya tidak ada alias 0, ingat aturan AVL/RBT, bahwa ssubtree kiri dan kanan hanya boleh seilsih maksimal 1 node, karena di kasus ini selisih 2, maka kita harus menyeimbangkannya kembali dengan menggunakan double rotation (left-right)

double rotation : step 1
rotasi 5 dan 6 dengan rotasi kiri, karena 5 ke 6 kanan, rotasi kebalikannya

double rotation : step 2
rotasi 6 dan 9, karena 9 ke 6 kiri, maka rotasi kanan
meskipun node 9 berubah warna pada step-step sebelumnya, akan tetapi warna node tidak berubah pada warna asal node sebelum node 8 dihapus

contoh 3 :

kita akan menghapus node 15. 

node 15 digantikan oleh anak kanan terkecilnya yaitu 20
pada penghapusan node kali ini mengikuti aturan ke 2, karena node yg dihapus berwarna hitam dan anak yang menggantikannya berwarna merah. oleh karena itu, 20 berubah warna menjadi hitam

contoh 4 :

kita akan menghapus node 12 yang berwarna hitam dan akan digantikan node 13

node 12 digantikan node 13 yang juga berwarna hitam maka ikuti aturan ke 3
pada gambar sebelumnya, kita dapat menentukan N = 13, P = 14, S = 20, Sl = 17 dan Sr = tidak ada
karena sibling hitam, dan anaknya ada yang merah maka mengikuti aturan 3c

rotasi dilakukan pada node 14 yang tidak seimbang.
kita melakukan single rotasi karena dari 14 ke 17 kanan dan 17 ke 20 kanan (right-right)

node 17 berubah warna menjadi merah dan node 14, 20 berubah menjadi warna hitam

2-3 Tree

2-3 tree adalah sebuah struktur data dimana setiap internal nodenya (non leaf) adalah 2-node atau 3-node dan semua leafnya berada pada level yang sama

• 2-node adalah suatu node yang memiliki 1 data dan 2 anak
• 3-node adalah suatu node yang memiliki 2 data dan 3 anak

data-data yang disimpan setiap node pada 2-3 tree harus sudah berurutan

contoh 2-3 Tree :

2-3 Tree Operations : Search  

operasi searching pada 2-3 tree sama seperti pada BST, sehingga hanya perlu membandingkan data yang dicari dengan data yang ada pada node. Misal K adalah node yang dicari dan N adalah node yang akan dibandingkan dengan tree, maka jika K lebih kecil dari N, operasi searching berlanjut ke subtree kiri N namun jika K lebih besar dari N, maka operasi searching berlanjut ke subtree kanan N. Ini terjadi terus-menerus sampai K = N, atau K ditemukan.

2-3 Tree Operations : Insertion

aturan insertion :

1. anggap node yang di insert adalah key
2. key akan ditempatkan pada leaf. a) jika leaf adalah 2-node, maka key dimasukan kedalam leaf sehingga leaf tersebut menjadi 3-node. b) jika leaf adalah 3-node, maka ambil nilai tengah dari A, B, dan key (A adalah data-1 pada leaf, dan B adalah data-2 pada leaf) dan push nilai tengah tersebut pada parentnya
3. jika pada saat aturan kedua parentnya bukanlah 2-node, melainkan 3-node, tentukan kembali nilai tengah lalu push kembali ke parentnya
4. jika pada saat aturan ke 2 dan 3 tidak bisa dilakukan karena parent sampai ke rootnya adalah 3-node, maka tentukan kembali nilai tengah, kemudian nilai tengah tersebut akan dibuat root baru.

contoh 1 :

insert node 45, kita akan mencari posisi yang tepat untuk 45, pada leaf di sebelah kanan 30. karena leaf tersebut merupakan 2-node, maka sesuai aturan ke 2a, 45 langsung diletakan pada leaf sehingga leaf membentuk 3-node

contoh 2 :

insert node 75, posisi yang tepat adalah di leaf pada sebelah kanan 70, namun leaf tersebut adalah 3-node, maka kita ikuti aturan 2b. Nilai tengah dari 75, 80 dan 90 adalah 80, karena 80>75 dan 80<90.
kita push 80 pada parentnya yaitu 2-node yang datanya 70.
karena parentnya adalah 2-node maka kita dapat langsung memasukan datanya

karena saat ini parent 70 berubah dari 2-node menjadi 3-node, maka ia harus memiliki 3 anak, sehingga 75 dan 90 kita pisahkan menjadi 2 anak. Jadilah demikian

contoh 3 :

insert 24, posisi yang tepat adalah di antara node 20 dan 30, karena 24>20 dan 24<30. namun leaf pada posisi tengah dari 20 dan 30 adalah 3-node, maka kita tentukan nilai tengah, yaitu 24, lalu push 24 ke parentnya. 

Akan tetapi parentnya juga merupakan 3-node (dengan data 20 dan 30), maka kita ikuti aturan ke-3, sehingga kita tentukan lagi nilai tengahnya, yaitu 24, lalu push 24 ke parentnya (parent dari parent) lagi. Parent tersebut merupakan 2-node dengan data 50, sehingga kita dapat langsung memasukan nilainya pada parent.

karena saat ini parentnya telah berubah menjadi 3-node, maka harus memiliki 3 anak, maka kita pisahkan 3-node sebelumnya menjadi 2 bagian. seperti pada gambar diatas.

contoh 4 :

insert 95, posisi yang tepat adalah leaf pada sebelah kanan 80, namun leaf tersebut adalah 3-node, sehingga kita harus menentukan nilai tengahnya, yaitu 95. lalu push pada parentnya

ternyata parentnya adalah 3-node lagi, maka kita tentukan nilai tengahnya lagi, yaitu 80, kemudian push pada parent dari parent nya kembali

parentnya merupakan 3-node, dan parentnya adalah root, sehingga tidak mungkin kita push ke parent dari parentnya lagi, karena root tidak memiliki parent, maka kita lakukan aturan ke-4. kita tentukan nilai tengahnya, yaitu 50, dan 50 tersebut kita jadikan root baru (2-node)

50 menjadi root 2-node, karena root berbentuk 2-node, maka harus memiliki 2 anak, maka kita pisahkan node-node yang ada dibawahnya menjadi demikian.

2-3 Tree Operations : Deletion

aturan deletion :

1. misal node yang dihapus adalah key
2. delete sama seperti  BST, yaitu digantikan oleh leafnya
3. jika leaf 3-node, maka ambil salah satu data untuk menggantikan key, seperti BST, terbesar dari subtree kiri atau terkecil dari subtree kanan
4. jika leaf 2-node, maka :

• jika parent dari leaf adalah 3-node, maka ambil satu data dari parent. kemudian kita perhatikan kembali siblingnya. a) jika sibling 3-node, maka ambil satu data kemudian push pada parent, agar parent kembali menjadi 3-node, b) jika sibling 2-node, maka biarkan parent menjadi 2-node, dan satukan node tersebut dengan siblingnya
• jika parent dari leaf adalah 2-node, kita perhatikan siblingnya. a) jika sibling 3-node, ambil satu data dari parent dan push satu nilai dari sibling ke parent. b) jika sibling 2-node, maka satukan sibling dengan parent.

contoh 1 :

kita akan menghapus 23, karena 23 adalah leaf, dan merupakan 3-node, maka hapus saja langsung. dan biarkan leaf berubah dari 3-node menjadi 2-node

menjadi demikian

contoh 2 :

delete 50, maka digantikan oleh anak kiri terbesar yaitu 40, karena 40 merupakan leaf 2 node, maka kita mengikuti aturan ke-4  yang pertama (karena parent dari 40 adalah 3-node).

40 menggantikan 50, lalu ambil salah satu dari parent, yaitu 30 (karena node yang kosong disebelah kanan, maka kita ambil yang terbesar dari 20 dan 30). karena siblingnya merupakan 2-node, maka kita ikuti aturan ke-4 pertama yang b

parent dibiarkan menjadi 2 node, dan kita satukan 30 dengan siblingnya yaitu disebelah kanan 25, karena tidak mungkin di kiri 15,dan diantara 15 dan 25 karena 30 lebih besar dari keduanya, sehingga diletakan paling kanan. Jadilah demiikian